[Paper] Interconnect Stack Parameter Optimization Using Genetic Algorithm [2/2]

Study

[Paper] Interconnect Stack Parameter Optimization Using Genetic Algorithm [2/2]

정선옥수수 2024. 5. 16. 08:51

이전 포스팅에서 Interconnect Stack Parameter Optimization Using Genetic Algorithm의 배경 지식까지 알아보았습니다.

배경 지식은 interconnect stack parameter가 회로에 미치는 영향과 논문에서 사용된 genetic algorithm에 대한 내용이 있었습니다.

이제는 제가 제안하는 방법과 결과를 다뤄보도록 하겠습니다.

먼저, 목차는 다음과 같습니다.

서론
배경 지식
제안 방법
- 매개변수 후보 선택 (candidate selection)
- 매개변수 필터링 (parameter filtering)
- 초기 샘플링 (initial sampling)
실험 결과

제안 방법

논문에서 제안하는 방법의 프로세스는 아래 그림과 같습니다.

Logic synthesis를 수행하여 얻은 netlist를 통해 프로세스가 시작됩니다.

Netlist는 initial physical synthesis를 수행하는 데 사용되어 initial physical design을 생성합니다.

Initial physical design를 기반으로 수행되는 parameter filtering은 어떠한 interconnect parameter가 회로 성능에 어떻게 영향을 미치는 지를 simulation 하고, 성능에 부정적인 parameter를 프로세스에서 제외합니다.

Candidate selection에서는 선정된 parameters의 값을 얼마나 조정할 것인지 시뮬레이션합니다.

예를 들어, metal layer 3 (M3)의 width를 증가시킬 것인데, 얼마까지 증가시키는 것이 좋을지 판단하는 것입니다.

너무 많이 증가시키다 보면, 비용이 개선치보다 지배적일 수 있기 때문에 이 과정을 수행합니다.

이전 포스팅에서 genetic algorithm은 환경 적합도가 높을수록 이후 세대로 더 잘 전달되도록 하는 과정임을 설명했습니다. 이는 반대로 보면 처음부터 환경 적합도가 높은 모집단을 형성하면 최적의 모집단을 형성하는 데 걸리는 시간이 크게 줄어들 것입니다. 이를 위해 initial sampling을 수행합니다.

최종적으로 initial population (초기 모집단)을 가지고 genetic algorithm을 수행합니다.

적합도는 frequency 개선량과 power consumption 개선량의 가중합으로 설정하여 최적화합니다.

적합도의 변화가 더 이상 관측되지 않으면 지금까지 얻었던 염색체 (parameter set) 중 적합도가 가장 높은 염색체를 선택됩니다.

Candidate selection

전체 방법 중 candidate selection에 대해서 아래 그래프를 가지고 설명하겠습니다.

논문에서 아래와 같은 각 candidate들은 이미 설정되어 있는 값의 정수배로 가정합니다.

그러면 w13인 M3에서 기본으로 설정되어 있는 width이고, 오른쪽으로 갈수록 두 배, 세 배 값이 됩니다.
$$w^1_3 , w^2_3, w^3_3, w^4_3 $$

그래프는 이전 포스팅의 RC model로 simulation 한 결과입니다.

왼쪽 그래프를 보면 width를 늘림에 따라서 resistance의 변화량이 점점 감소하는 것을 볼 수 있고, 오른쪽 그래프를 보면 capacitance가 선형적으로 증가하는 것을 볼 수 있습니다.

이를 통해 생각해 보면, width를 늘리는 것은 R에서 이득, C에서 손해를 본다는 것을 알 수 있습니다.

그런데 width를 늘리다 보면 R의 감소폭이 점점 줄어들게 되고, 결국 C의 증가폭과 trade-off 하는 구간이 발생합니다.

따라서 논문에서는 R, C 변화량이 동일해지는 지점을 기준으로 parameter candidate를 설정합니다.

이 그림에서는 w13, w23, w33이 candidate로 선정됩니다.

Parameter filtering

Parameter filtering은 최적화 과정에서 회로 성능에 부정적인 성능을 미칠 parameter를 예측하고, 최적화 이전에 제외하는 과정입니다. 이 과정에 대해서 아래의 그림을 보면서 이야기해 보겠습니다.

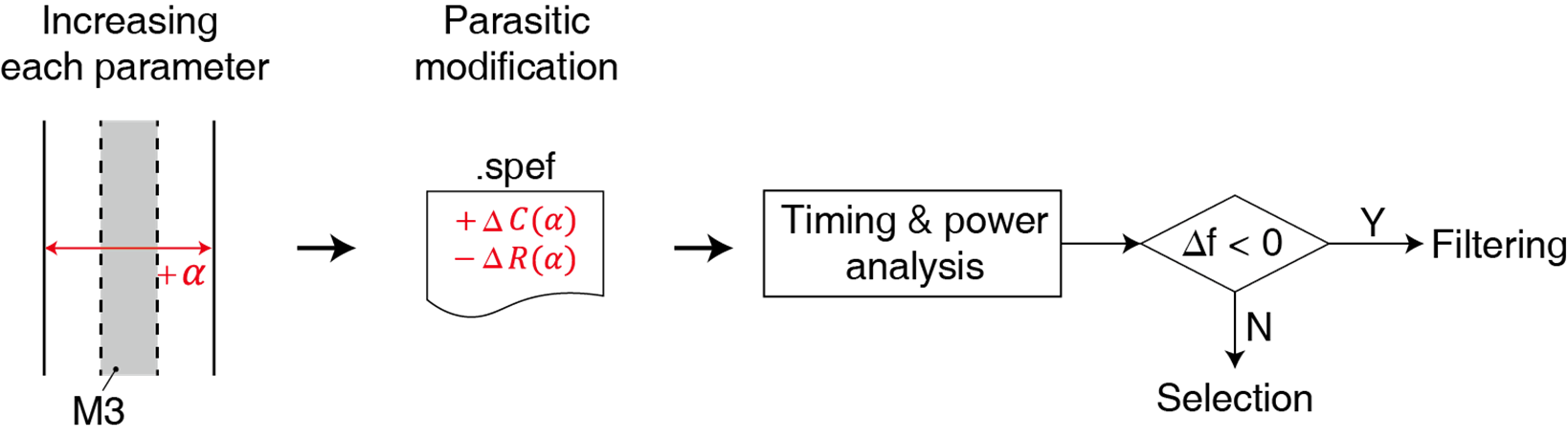
이 과정은 기존의 회로에서 특정 parameter (그림에서는 M3 width)의 값을 약간 증가시키는 것으로 시작됩니다.

그림처럼 α만큼 width를 증가시키면, 당연히 회로 내부에서 RC 값의 변화가 생깁니다.

이 변화한 RC 값을 다시 뽑는 과정은 다시 physical synthesis를 해야 해서 시간이 오래 걸립니다.

이 때문에 논문에서는 초기 physical synthesis로 얻은 standard parasitic exchange format (spef) file의 RC 정보를 직접 바꾸는 것으로 이러한 시간을 단축시킵니다.

EDA tool을 사용하면 정확한 RC 값을 얻을 수는 있지만 우리는 회로 성능에 어떤 영향을 미치는 지만 판단하면 되기에 대략적인 simulation만으로도 원하는 작업을 수행할 수 있습니다.

여기서 simulation은 이전 포스팅의 RC model을 사용합니다.

spef fiile을 업데이트했다면, 이를 입력으로 timing & power analysis를 수행하여 frequency와 power를 출력합니다.

그리고 freq와 power의 가중합으로 구성한 fitness가 parameter를 변경하기 전과 비교했을 때, 어떤지를 평가합니다.

Fitness의 변화량이 0보다 작다는 것은 회로 성능에 부정적인 영향을 미치는 것이므로 최적화에서 제외합니다.

이렇게 선정된 parameters를 가지고 다음 단계로 넘어갑니다.

Initial sampling

Initial sampling은 pararmeter filtering과 이어지면서 genetic algorithm을 수행하기 전에 최적에 가까운 initial population을 생성하는 작업입니다. 아래의 그림을 참고하면서 이야기해 보겠습니다.

이 방법은 parameter filtering에서 얻은 Δfitness(fitness 변화량)를 활용합니다.

큰 시간적인 비용을 들이지 않고, 최적에 가까운 parameter sets을 얻기 위해서는 이전의 결과를 활용하는 것이 효율적이기 때문입니다.

이제 그림을 보면서 설명하면, 가장 먼저 fitness scaling을 수행해 줍니다.

만약 M3, M4에 대한 width와 space를 고려한다고 가정해 보면, 우리는 각 parameter에 대한 Δfitness를 가집니다.

이 중 fitness를 크게 변화시킨 것도 있고 작게 변화시킨 것도 있을 것입니다.

이들을 0~1 사이로 정규화시켜 주면 fitness scaling 부분의 그림과 같이 각 parameter들의 Δfitness가 나열됩니다.

이제 정규화된 각 fitness를 각 parameter의 candidate 범위에 mapping을 해줍니다.

Mapping 된 위치를 평균(μ)으로 사용해 정규 분포를 그려주는데, 여기서 분산(σ)은 각 candidate의 차이로 설정합니다.

이제 생성된 각 parameter의 정규 분포에서 랜덤으로 값을 추출하여 initial parameter sets (initail population)을 생성합니다.

이후로는 genetic algorithm을 사용하여 새로운 population을 형성하는 과정을 반복합니다.

과정 중 Δfitness가 더 이상 변하지 않으면 모든 프로세스를 종료합니다.

실험 환경

결과를 이야기하기 전에 실험을 수행한 환경을 간단하게 집고 가겠습니다.

Parameters: M3 ~ M5의 metal width & space
Tools
- Logic synthesis: design compiler
- Physical synthesis: IC compiler1
- SPEF modification: starRCXT
- Timing & power analysis: Primetime
Programming language: shell, tcl, python3

결과

다음 표는 제안하는 방법과 기존 방법들로 실험을 했을 경우의 결과입니다.

먼저 표에서 주목해야 할 것은 제안 방법과 기존 genetic algorithm만 사용했을 때의 성능 평균입니다.

논문에서는 candidate selection, parameter filtering, initial samplinig 등을 사용하여 기존 방법보다 평균 freq. 가 0.3%, 평균 power가 0.6%가량 더 향상되었습니다.

여기서 사용된 sample은 얼마나 physical synthesis를 수행했는지와 같은데, 기존 genetic과 제안 방법은 동일한 수준의 sample을 사용했습니다.

제안 방법의 성능은 어느 정도의 sample을 사용해야 달성할 수 있는지는 random sampling에서 확인할 수 있습니다.

400개의 sample을 사용했을 경우, 평균적으로 제안 방법과 동일한 수준의 성능을 달성했습니다.

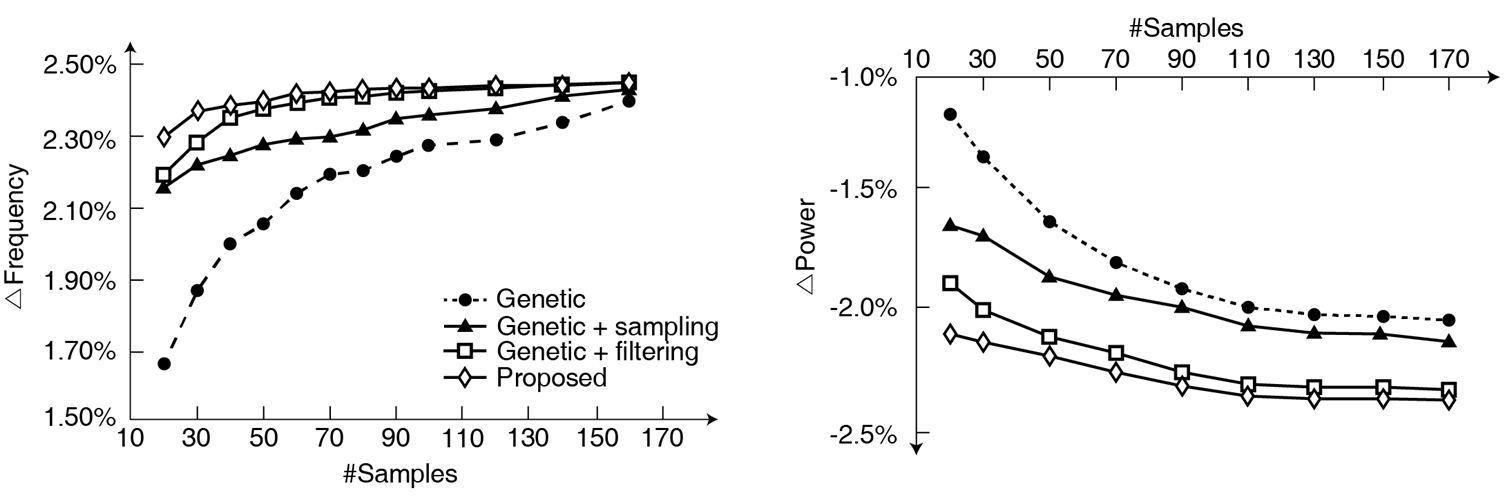
다음으로 볼 그래프는 특정 회로에서 sample의 수에 따라서 freq.와 power가 어떻게 변하는 지를 보여줍니다.

Freq. 의 경우, 제안 방법은 20개의 sample만으로 기존 genetic이 150개의 sample을 사용했을 때와 동일한 성능 향상을 달성했습니다.

이를 통해 회로 속도 측면에서는 제안 방법이 기존 방법보다 수렴속도가 약 7배가량 빠른 것을 알 수 있습니다.

Power의 경우, 각각의 방법을 적용할수록 성능 그래프가 점점 좋아지는 것을 볼 수 있습니다.

사실 수렴속도가 좋아졌다고는 하나 실제로 filtering, sampling 과정에서 추가되는 runtime이 존재하기에 그 부분도 고려해야 합니다.

위 그래프는 각 세대가 증가함에 따라서 filtering과 sampling이 runtime에서 차지하는 비중을 나타냅니다.

보통 약 5번의 세대 교체를 이루면 최적화가 완료되었는데, 이를 기점으로 보았을 때, runtime의 증가는 약 5% 임을 알 수 있습니다.

제가 제출했던 논문의 설명은 여기까지 입니다.

사실 제가 자꾸 내용을 까먹어서 메모한다는 생각으로 쓰다 보니 조금 말이 안 되는 부분이 있는데, 이 부분들은 다시 읽어보면서 고쳐나갈 계획입니다.

사실 결과가 눈에 띄게 좋진 않지만 그래도 큰 비용을 들이지 않고 성능을 향상할 수 있다는 부분에서 나름 의미가 있는 연구였다고 생각합니다.